ANOVA1Way
Advanced Analysis Library Only
AnalysisLibErrType ANOVA1Way (double observationsArray[], ssize_t levelArray[], ssize_t totalObservations, ssize_t totalLevels, double *sumOfSquaresF, double *meanSquareF, double *fValue, double *significance, double *sumOfSquaresRF, double *meanSquareRF, double *totalSumOfSquares);
Purpose
Takes an array of experimental observations you make at various levels of some factor, with at least one observation per factor, and performs a one-way analysis of variance (ANOVA) in the fixed effect model.
The one-way analysis of variance is a test to determine whether the level of the factor has an effect on the experimental outcome.
| For the following sections, let | observationsArray = y |
| levelArray = level | |
| totalObservations = n | |
| totalLevels = k | |
| sumOfSquaresF = ssa | |
| meanSquareF = msa | |
| fValue = f | |
| significance = sig | |
| sumOfSquaresRF = sse | |
| meanSquareRF = mse | |
| totalSumOfSquares = tss |
Factors and Levels
A factor is a way of categorizing data. You can categorize data into levels, beginning with level 0. For example, if you perform a measurement on individuals, such as counting the number of sit-ups they can perform, one such categorization method is age. For age, you might have three levels, as shown in the following table.
| Level | Ages |
|---|---|
| 0 | 6 years to 10 years |
| 1 | 11 years to 15 years |
| 2 | 16 years to 20 years |
General Method
Break up the total sum of squares, a measure of the total variation of the data from the overall population mean, into component sums of squares, which might be attributed to different sources.
You now have:
tss = ssa + sse
| where | sumOfSquaresF is a measure of variation that is attributed to the factor |
| sumOfSquaresRF is a measure of variation that is attributed to random fluctuation |
Divide by appropriate numbers to obtain the averages msa and mse. If the factor causes much variation, msa will be larger relative to mse. The ratio f also will be larger relative to mse.
If the null hypothesis is true, the ratio f is taken from an F-distribution with k – 1 and n – k degrees of freedom, from which you can calculate probabilities. Given a particular f, sig is the probability that sampling from this distribution results in a value larger than f.
Statistical Model
ANOVA1Way expresses each experimental outcome as the sum of three parts while it performs the analysis of variance. Let yi, m be the mth observation from the ith level. Each observation is written as
yi, m = μ + αi + εi, m
| where | μ is a standard effect |
| αi is the effect of the ith level of the factor | |
| εi, m is a random fluctuation |
Assumptions
Assume that the populations of measurements at each level are normally distributed with mean αi and variance σ2A. Assume that the means αi sum to zero. Finally, assume that for each i and m, εi, m is normally distributed with mean 0 and variance σ2A.
Hypothesis
Test the null hypothesis that αi = 0 for i = 0, 1, . . ., k – 1, where totalLevels is the total number of levels. In other words, assume from the start that the levels have no effect on the experimental outcome, then look for evidence to the contrary.
Testing the Hypothesis
ANOVA1Way generates a number f so that if the hypothesis is true, that number is from an F-distribution with k – 1 and n – k degrees of freedom. ANOVA1Way also calculates the probability that a number taken from this F-distribution is larger than f. This is the output parameter significance:
sig = prob(x > f) where x is from F(k – 1, n – k)
Use the probability sig to determine when to reject the hypothesis by choosing a level of significance for the hypothesis. The level of significance determines how likely you are to reject the hypothesis when it is in fact true. Thus, the level of significance should be small, for example, 0.05. Remember that the smaller the level of significance, the less likely you are to reject the hypothesis.
Reject the hypothesis when the output parameter significance is less than the level of significance you choose.
Formulas
Let yi, m be the mth observation at the ith level for m = 0, 1, ..., ni and i = 0, 1, . . ., k.
Let ni = the number of observations at the ith level.
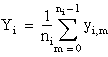
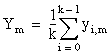
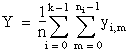
T = n × Y
Then:
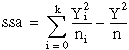
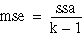
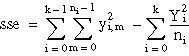
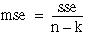
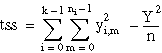
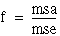where fValue is from an F-distribution with k – 1 and n – k degrees of freedomeExample Scenario
Suppose that researchers want to know whether the amount of rainfall affects the yield of a crop. The factor, rainfall, is divided into three levels (k = 3) as shown in the following table.
| Level | Rainfall (Factor) |
|---|---|
| 0 | 2 inches |
| 1 | 3 inches |
| 2 | 4 inches |
The researchers set up 10 plots in various geographical locations chosen so that each plot receives a different amount of rainfall. The following table shows their results.
| Level | Bushels produced from each plot |
|---|---|
| 0 | 128 122 126 124 |
| 1 | 140 141 143 |
| 2 | 120 118 123 |
To perform a one-way analysis using ANOVA1Way, you store all the numbers of bushels in a double-precision array y of size 10. The integer array level records the levels in which observations were made. For any particular i, you must set these arrays such that yi is the number of bushels a plot produces in the ith level. For example,
leveli = 0
yi = 128, 122, 126, or 124
are valid combinations. Therefore, you can set up the input arrays y and level in this example for ANOVA1Way as follows:
y = 128, 122, 126, 124, 140, 141, 143, 120, 118, 123
level = 0, 0, 0, 0, 1, 1, 1, 2, 2, 2
Running the code in the following example produces:
sig = 0.0000239
For a level of significance such as 0.05, the ANOVA1Way results show that the researchers must reject the hypothesis that the rainfall has no effect on the crop yield. In other words, the rainfall does affect the crop yield.
Example Code
double y[10], ssa, msa, f, sig, sse, mse, tss;
int level[10];
int k;
int status;
k = 3; /* three levels for rainfall */
/* Read in recorded data y(10), level[10]. */
status = ANOVA1Way(y, level, 10, k, &ssa, &msa, &f, &sig, &sse, &mse, &tss);
Parameters
| Input | ||
| Name | Type | Description |
| observationsArray | double [] | An array of experimental observations. |
| levelArray | ssize_t [] | The ith element tells in what level of the experimental factor the ith observation falls. The range of values in levelArray is from zero to (totalLevels – 1). |
| totalObservations | ssize_t | Total number of experimental observations. |
| totalLevels | ssize_t | Total number of different levels that the experimental factor assumes. |
| Output | ||
| Name | Type | Description |
| sumOfSquares_F | double | Sum of squares as a result of the factor. This value is from a chi-square distribution of (totalLevels – 1) degrees of freedom. |
| meanSquare_F | double | The mean square error as a result of the factor. |
| f_Value | double | Calculated F-value. |
| significance | double | Level of significance at which you must reject the null hypothesis. |
| sumOfSquares_RF | double | Sum of squares as a result of random fluctuation. |
| meanSquare_RF | double | The mean square as a result of random fluctuation. |
| totalSumOfSquares | double | Total sum of squares. |
Return Value
| Name | Type | Description |
| status | AnalysisLibErrType | A value that specifies the type of error that occurred. Refer to analysis.h for definitions of these constants. |
Additional Information
Library: Advanced Analysis Library
Include file: analysis.h
LabWindows/CVI compatibility: LabWindows/CVI 3.1 and later