ANOVA2Way
Advanced Analysis Library Only
AnalysisLibErrType ANOVA2Way (double observationsArray[], ssize_t levelAArray[], ssize_t levelBArray[], ssize_t totalObservations, ssize_t cellCount, ssize_t levelsInA, ssize_t levelsInB, double information[4][4], double *significanceA, double *significanceB, double *significanceAB);
Purpose
Takes an array of experimental observations made at various levels of two factors and performs a two-way analysis of variance in any of the following models:
- Model 1—Fixed effects with no interaction and one observation per cell. cellCount = 1 per specified levels levelsInA and levelsInB of the factors A and B, respectively.
- Model 2—Fixed effects with interaction and cellCount > 1 observations per cell.
- Model 3—Either of the mixed-effects models, where one factor is taken to have a fixed effect but the other is taken to have a random effect, with interaction and cellCount > 1 observations per cell.
- Model 4—Random effects with interaction and cellCount > 1 observations per cell.
Any ANOVA looks for evidence that the factors, or interactions among the factors, have a significant effect on experimental outcomes. The method for finding significance varies among models.
| For the following sections, let | observationsArray = y |
| levelA_Array = levelA | |
| levelB_Array = levelB | |
| totalObservations = N | |
| cellCount = L | |
| levelsInA = a | |
| levelsInB = b | |
| information = info | |
| significanceA = sigA | |
| significanceB = sigB | |
| significanceAB = sigAB |
Factors, Levels, and Cells
A factor is a way of categorizing data. You can categorize data into levels, beginning with level 0. For example, if you perform a measurement on individuals, such as counting the number of sit-ups they can perform, one such categorization method is age. For age, you might have three levels, as shown in the following table.
| Level | Age |
|---|---|
| 0 | 6 years to 10 years |
| 1 | 11 years to 15 years |
| 2 | 16 years to 20 years |
Another possible factor is eye color, with the levels shown in the following table.
| Level | Eye Color |
|---|---|
| 0 | blue |
| 1 | brown |
| 2 | green |
| 3 | hazel |
In this example, an analysis of variance seeks evidence that the ages and eye color of the subjects have an effect on the number of sit-ups they perform.
A cell of data consists of all those experimental observations that fall in particular levels of the two factors. In this instance, a cell might consist of those observations made on hazel-eyed individuals between 11 and 15 years old. The number of observations that fall in each cell must be a constant number L that does not vary between cells.
Random and Fixed Effects
A factor is taken as a random effect when the factor has a large population of levels you want to draw conclusions about, but that you cannot sample at all levels. Levels are sampled at random in the hope of generalizing about all levels.
A factor is taken as a fixed effect when you can sample the factor from all levels you want to draw conclusions about.
The input parameters a and b represent the number of levels in factors A and B, respectively. If factor A is random, set a to a negative value. If factor B is random, set b to a negative value. If only one observation per cell exists, both a and b must be positive. Use model 1 as previously described.
General Method
Each of the previous models breaks up the total sum of squares, which is a measure of the total variation of the data from the overall population mean, into a number of component sums of squares. In model 1:
tss = ssa + ssb + sse
whereas in models 2 through 4:
tss = ssa + ssb + ssab + sse
Each component of the sums is a measure of variation attributed to a certain factor or interaction among the factors. The component ssa is a measure of the variation as a result of factor A; ssb is a measure of the variation as a result of factor B; ssab is a measure of the variation as a result of the interaction between factors A and B; and sse is a measure of the variation as a result of random fluctuation. Notice that there is no ssab term with model 1. Thus, no interaction exists.
If factor A has a strong effect on the experimental observations, msa is relatively large. You can look at specific ratios of these averages because you know how they are statistically distributed. You can therefore determine how likely it is that factor A is as relatively large as it is.
Statistical Model
Let yp, q, r be the rth observation at the pth and qth levels of A and B, respectively, where r = 0, 1, . . ., L – 1.
In model 1, express each observation as the sum of four components so that:
yp, q, r = μ + αp + βq + εp, q, r
| where | μ represents a standard effect present in each observation |
| αp represents the effect of the pth level of factor A | |
| βq represents the effect of the qth level of factor B | |
| εp, q, r is a random fluctuation |
In models 2 through 4, express each observation as the sum of five components so that:
yp, q, r = μ + αp + βq + (αβ)p, q + εp, q, r
| where | μ represents a standard effect present in each observation |
| αp represents the effect of the pth level of factor A | |
| βq represents the effect of the qth level of factor B | |
| εp, q, r is a random fluctuation | |
| (αβ)p, q represents the effect of the interaction between the pth level of factor A and the qth level of factor B |
Assumptions
- Assume that for each p, q, and r, εp, q, r is normally distributed with mean 0 and variance σ2ε.
- If a factor such as A is fixed, assume that the populations of measurements at each level are normally distributed with mean αp and variance σ2A. All the populations at each of the levels have the same variance. In addition, assume that all the αp means sum to zero. Make an analogous assumption for B.
- If a factor such as A is random, assume that the effect of the level of A itself, αp, is a random variable normally distributed with mean 0 and variance σ2A. Make an analogous assumption for B.
- If all the factors, such as A and B, associated with the effect of an interaction (αβ)p, q are fixed, assume that the populations of measurements at each level are normally distributed with mean (αβ)p, q and variance σ2AB. For any fixed p, the (αβ)p, q means sum to zero when summing over all q. Similarly, for any fixed q the (αβ)p, q means sum to zero when summing over all p.
- If any of the factors, such as A and B, associated with the effect of an interaction (αβ)p, q are random, assume that the effect is a random variable normally distributed with mean 0 and variance σ2AB. If A is fixed but B is random, assume also that for any fixed q, the (αβ)p, q means sum to zero when summing over all p. Similarly, if B is fixed but A is random, assume also that for any fixed p, the (αβ)p, q means sum to zero when summing over all q.
- Assume that all effects taken to random variables are independent.
Hypotheses
Each of the following hypotheses are different ways of stating that a factor or an interaction among factors has no effect on experimental outcomes. Start by assuming that there are no effects and then seek evidence to contradict these assumptions. The three hypotheses are as follows:
- For hypothesis A, ap = 0 for all levels of p if factor A is fixed; σ2A = 0 if factor A is random.
- For hypothesis B, βq = 0 for all levels of q if factor B is fixed; σ2B = 0 if factor B is random.
- For hypothesis AB, (αβ)p, q for all levels of p and q if factors A and B are fixed; σ2AB = 0 if either factor A or factor B is random. This does not apply to model 1, where no interaction exists and the associated output parameters are superfluous.
Testing the Hypotheses
For each hypothesis, ANOVA2Way generates a number so that if the hypothesis is true, that number is from a particular F-distribution.
For example, in model 1, fa = msa/mse, associated with hypothesis A, is from an F-distribution with a – 1 and (a – 1) × (b – 1) degrees of freedom, given that hypothesis A is true. In models 2 through 4, fa = msa/mse, associated with hypothesis A, is from an F-distribution with a – 1 and ab(L – 1) degrees of freedom, given that hypothesis A is true. ANOVA2Way calculates the probability that a number taken from a particular F-distribution is larger than the F-value. For example:
sigA = prob(X > fa) where X is from F(a – 1, (a – 1)(b – 1))
Use the probabilities sigA, sigB, and sigAB to determine when to reject the associated hypotheses A, B, and AB by choosing a level of significance for each hypothesis. The level of significance determines how likely you are to reject the hypothesis when it is in fact true. Thus, the level of significance should be small, for example, 0.05. Remember that the smaller the level of significance, the less likely you are to reject the hypothesis.
Reject a particular hypothesis when the associated output parameter sigA, sigB, or sigAB is less than the level of significance you chose for that hypothesis. If A is a random effect, the chosen level of significance is 0.05, and sigA = 0.03, you must reject the hypothesis that σ2A and conclude that factor A has an effect on the experimental observations.
Formulas
Let yp, q, r be the rth observation at the pth and qth levels of A and B, respectively, where R = 0, 1, . . ., L – 1.
Let:
aa = |a|
bb = |b|

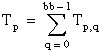
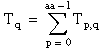
T = the total sum of all observations:
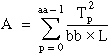
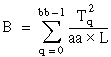
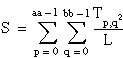
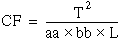
Then
ssa = A – CF

ssb = B – CF
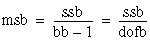
ssab = S – A – B – CF
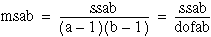
sse = T – S
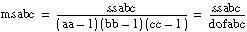

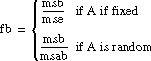
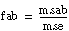
If 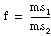
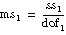
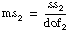
assume that f is from an F-distribution with dof1 and dof2 degrees of freedom.
Example Scenario
Suppose that researchers want to know how the amount of rainfall and the average temperature affect the yield of a crop. Each factor, rainfall and temperature, is divided into three levels as shown in the following tables of rainfall and temperature levels.
| Level | Rainfall (Factor A) |
|---|---|
| 0 | 2 inches |
| 1 | 3 inches |
| 2 | 4 inches |
| Level | Temperature (Factor B) |
|---|---|
| 0 | 76 – 80 degrees |
| 1 | 81 – 85 degrees |
| 2 | 86 – 90 degrees |
A particular plot planted with the crop might appear in any one of the nine different combinations of these levels with the two factors. For example, one combination might be 2 inches of rain and an average temperature between 76 degrees and 80 degrees, recorded as (0,0). Call these combinations cells.
The researchers set up 18 plots in various geographical locations chosen so that two plots fall in each of the nine cells. To measure the productivity of a particular plot, they record the crop production. Let rainfall be factor A and temperature be factor B. The following table shows their results.
| (A, B) | Bushels produced from each plot |
|---|---|
| (0, 0) | 128 122 |
| (0, 1) | 113 108 |
| (0, 2) | 116 116 |
| (1, 0) | 132 129 |
| (1, 1) | 119 121 |
| (1, 2) | 126 113 |
| (2, 0) | 118 114 |
| (2, 1) | 141 133 |
| (2, 2) | 121 123 |
To perform a two-way analysis of variance in the fixed-effect model using ANOVA2Way, you store all the numbers of bushels in a double-precision array y of size 18. The integer arrays levelA and levelB record the cells in which observations were made. For any particular i, you set these arrays such that yi is the number of bushels a plot produces in the (levelAi, levelBi) cell. For example:
(levelAi, levelBi) = (0, 1)
yi = 113 or 108
are valid combinations. Therefore, you can set up the input arrays y, levelA, and levelB in this example for ANOVA2Way as follows:
y = 128, 122, 113, 108, 116, 132, 129, 119, 121, 126, 113, 118, 114, 141, 133, 121, 123
levelA = 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2
levelB = 0, 0, 1, 1, 2, 2, 0, 0, 1, 1, 2, 2, 0, 0, 1, 1, 2, 2
Running the code in the following example produces:
sigA = 0.026
sigB = 0.203
sigAB = 0.0018
For a level of significance such as 0.05, the ANOVA2Way results show that the researchers cannot reject the hypotheses that the combination of rainfall and temperature has any effect on the crop yield. In other words, the combination of rainfall and temperature has a significant effect on crop yield.
Example Code
double y[18], sigA, sigB, sigAB, info[4][4];
int levelA[18], levelB[18];
int L, a, b;
int status;
L = 2; /* two observations per cell */
a = 3; /* three levels for factor A, Rainfall */
b = 3; /* three levels for factor B, Temperature */
/* Read in recorded data y[18], levelA[18], levelB[18]. */
status = ANOVA2Way(y, levelA, levelB, 18, L, a, b, info, &sigA, &sigB, &sigAB);
Parameters
| Input | ||
| Name | Type | Description |
| observationsArray | double [] | Array of experimental observations. The number of elements in this array should be |levelsInA| × |levelsInB| × cellCount elements. |
| levelAArray | ssize_t [] | The ith element tells in what level of the experimental factor A the ith observation falls. The number of values in levelA_Array should total cellCount × levelsInA × levelsInB. |
| levelBArray | ssize_t [] | The ith element tells in what level of the experimental B the ith observation falls. The number of values in levelB_Array should total cellCount × levelsInA × levelsInB. |
| totalObservations | ssize_t | Total number of experimental observations. The number of values in totalObservations should total cellCount × levelsInA × levelsInB. |
| cellCount | ssize_t | Number of observations per cell. Observations made at particular levels x and y of A and B respectively, are said to fall in the (x,y) cell. cellCount is the number of observations recorded at those levels of A and B. |
| levelsInA | ssize_t | Number of levels in factor A. If factor A is a fixed effect, then levelsInA > 0. If factor A is a random effect, then levelsInA < 0. |
| levelsInB | ssize_t | Number of levels in factor B. If factor B is a fixed effect, then levelsInB > 0. If factor B is a random effect, then levelsInB < 0. |
| Output | ||
| Name | Type | Description |
| information | double [][4] | A 4-by-4 matrix as follows: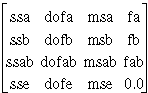
where ss designates sums of squares, dof designates degrees of freedom of ss, ms designates mean squares, and f designates F-distributions, depending on the statistical model. Column 0 holds the 4 sums of squares due to a, b, ab interaction, and random fluctuation. Column 1 holds the degrees of freedom of the respective sums of squares (considered as chi-square distributed random variables). Column 2 contains the 4 corresponding mean squares. Column 3 contains the 3 corresponding F-values and a 0.0. |
| significanceA | double | Level of significance at which you must reject hypothesis A. |
| significanceB | double | Level of significance at which you must reject hypothesis B. |
| significanceAB | double | Level of significance at which you must reject hypothesis AB. |
Return Value
| Name | Type | Description |
| status | AnalysisLibErrType | A value that specifies the type of error that occurred. Refer to analysis.h for definitions of these constants. |
Additional Information
Library: Advanced Analysis Library
Include file: analysis.h
LabWindows/CVI compatibility: LabWindows/CVI 3.1 and later