Contingency_Table
Advanced Analysis Library Only
AnalysisLibErrType Contingency_Table (int s, int k, void *contingencyTable, double *testStat, double *significance);
Purpose
Creates a contingency table in which to classify and tally objects of experimentation according to two schemes of categorization. Use Contingency_Table to perform a test of homogeneity or a test of independence.
 |
Note For both tests, the math is identical. It is not necessary to specify which test you apply. The only difference is in the hypothesis you test. |
A contingency table is a table in which you can classify and tally objects of experimentation according to two schemes of categorization. For example, if the objects of experimentation are individuals, one scheme might be political affiliation: Know-Nothing, Tory, Whig, Mugwump, and so on. Another scheme might be to classify individuals according to how they vote on an issue.
Chi-Square Test of Homogeneity
Take a random sample of a fixed size from each of the categories in one categorization scheme for the chi-square test of homogeneity. For each of the samples, categorize the objects of experimentation according to the second scheme and tally them. For example, you might pick 100 Know-Nothings, 100 Whigs, 100 Tories, and 100 Mugwumps. Count the number of individuals who vote a certain way for each category. This produces the contingency table shown in the following table.
| Category | Yes | No | Undecided |
|---|---|---|---|
| Know-Nothing | 36 | 24 | 40 |
| Whig | 12 | 53 | 35 |
| Tory | 61 | 11 | 28 |
| Mugwump | 83 | 3 | 14 |
Notice that the sum of each of the rows equals 100.
Test the hypothesis that the populations from which you take each sample are identically distributed with respect to the second categorization scheme. For example, you can test the hypothesis that the four samples of politically affiliated individuals are distributed identically with respect to the way they vote. If this hypothesis is true, it means that a Mugwump you select at random is just as likely to vote yes as a Whig you select at random.
Chi-Square Test of Independence
Take only one sample from the total population for the chi-square test of independence. Categorize each object of experimentation and tally them in the two categorization schemes. If you select 500 individuals, for example, you might receive the results in the contingency table shown in the following table.
| Category | Yes | No | Undecided |
|---|---|---|---|
| Know-Nothing | 18 | 15 | 18 |
| Whig | 55 | 93 | 38 |
| Tory | 101 | 83 | 20 |
| Mugwump | 16 | 31 | 12 |
Notice that the sum of each row is different but that the total number of individuals tallied is 500.
Testing the Hypothesis
Test the hypothesis that the categorization schemes are independent. For example, if you choose a person at random and he or she is a Mugwump, the hypothesis states that his or her political affiliation has no effect on how he or she votes on the issue you select.
Whichever test you use, you must choose a level of significance. This determines how likely you are to reject a true hypothesis. Thus, the level of significance should be small, for example, 0.05.
The significance parameter is the level of significance at which you reject the hypothesis:
significance = Prob(χ ≥ testStat)
where χ is a random variable from the chi-square distribution with (s – 1) × (k – 1)
If significance is less than the level of significance, you must reject the hypothesis.
Formulas
Let yp, q be the number of occurrences in the (p, q)th cell of the contingency table for p = 0, 1, . . ., (s – 1) and q = 0, 1, . . ., (k – 1).
Let:
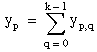
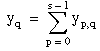
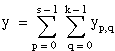
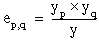
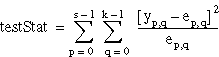
Example Code
/* Generate a random contingency table. Because rows will not have identical sums, use the chi-square test of independence. */
int s=10, k=10, y[10][10], i, j, status;
double Test_Stat, Sig, temp[1];
for(i=0; i<s; i++)
for(j=0; j<k; j++)
{
WhiteNoise (1, 5, 17, temp);
temp[0] += 6.0;
y[i][j] = (int) temp[0];
}
status = Contingency_Table (s, k, y, &Test_Stat, &Sig);
Parameters
| Input | ||
| Name | Type | Description |
| s | int | Number of random samples in the test of homogeneity or the number of categories in the first categorization scheme in the test of independence. |
| k | int | Number of categories in the test of homogeneity or the number of categories in the second categorization scheme in the test of independence. |
| contingencyTable | void * | Contingency table, indexed as an s-by-k matrix. In the chi-square test of homogeneity, the rows tally objects in separate samples, while the columns tally objects in different categories. In the chi-square test of independence, the rows tally objects according to one categorization scheme, while the columns tally objects according to another categorization scheme. This table must be an array of integers. |
| Output | ||
| Name | Type | Description |
| testStat | double | Use to calculate Sig. If the hypothesis is true, testStat is known to come from a chi-square distribution with (s – 1) × (k – 1) degrees of freedom. |
| significance | double | Level of significance at which you must reject the hypothesis. significance = Prob(X ≤ testStat) where X is a random variable from the chi-square distribution with (s – 1) × (k – 1) degrees of freedom. |
Return Value
| Name | Type | Description |
| status | AnalysisLibErrType | A value that specifies the type of error that occurred. Refer to analysis.h for definitions of these constants. |
Additional Information
Library: Advanced Analysis Library
Include file: analysis.h
LabWindows/CVI compatibility: LabWindows/CVI 3.1 and later