CorrelateEx
Advanced Analysis Library Only
AnalysisLibErrType CorrelateEx (double arrayX[], ssize_t sizeOfX, double arrayY[], ssize_t sizeOfY, int algorithm, double outputArray[]);
Purpose
Finds the correlation of the input arrays. National Instruments recommends that you use this function instead of Correlate. CorrelateEx includes an additional parameter, which makes it more versatile than Correlate.
The cross correlation Rxy(t) of the sequences x(t) and y(t) is defined by the following equation:
where the symbol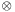 
denotes correlation.
The discrete implementation of this function is as follows. Let h represent a sequence whose indexing can be negative, let N be the number of elements in the input sequence arrayX, let M be the number of elements in the sequence arrayY, and assume that the indexed elements of arrayX and arrayY that lie outside their range are equal to zero, as shown by the following equations:
xj = 0, j < 0 or j ≥ N
and
yj = 0, j < 0 or j ≥ M.
Then CorrelateEx obtains the elements of h using the following equation:
for j = -(N–1), -(N–2), ..., -1, 0, 1, ..., (M–2), (M–1)
The elements of the output sequence outputArray are related to the elements in the sequence h byRxyi = hi – (N–1)
for i = 0, 1, 2, ..., N+M–2.
Because you cannot index LabWindows/CVI arrays with negative numbers, the corresponding cross correlation value at t = 0 is the Nth element of the output sequence outputArray. Therefore, outputArray represents the correlation values that CorrelateEx shifts N times in indexing.
 |
Note This function temporarily allocates memory for use as a work area. If CorrelateEx cannot allocate memory, the function returns an error code. |
Parameters
| Input | |||||||||||
| Name | Type | Description | |||||||||
| arrayX | double [] | First input array. | |||||||||
| sizeOfX | ssize_t | Number of elements in arrayX. | |||||||||
| arrayY | double [] | Second input array. | |||||||||
| sizeOfY | ssize_t | Number of elements in arrayY. | |||||||||
| algorithm | int | Specifies the correlation method to use. algorithm must be one of the following values. Note that slight numerical differences can exist between the two methods.
|
|||||||||
| Output | |||||||||||
| Name | Type | Description | |||||||||
| outputArray | double [] | The correlation of arrayX and arrayY. This array must be at least (n + m – 1) elements long. | |||||||||
Return Value
| Name | Type | Description |
| status | AnalysisLibErrType | A value that specifies the type of error that occurred. Refer to analysis.h for definitions of these constants. |
Additional Information
Library: Advanced Analysis Library
Include file: analysis.h
LabWindows/CVI compatibility: LabWindows/CVI 9.0 and later