CxSpecialMatrix
Advanced Analysis Library Only
AnalysisLibErrType CxSpecialMatrix (int matrixType, ssize_t identityMatrixSize, NIComplexNumber inputArray1[], ssize_t sizeOfArray1, NIComplexNumber inputArray2[], ssize_t sizeOfArray2, void *outputMatrix);
Purpose
Generates a special type of complex matrix depending on the value of matrixType. There are five possible matrix types: Identity, Diagonal, Toeplitz, Vandermonde, and Companion.
Parameters
| Input | ||||||||||||||||||||
| Name | Type | Description | ||||||||||||||||||
| matrixType | int | Type of matrix to generate. The following table shows each matrix type and its behavior. Let n represent matrixSize, x represent inputArray1, nx represent sizeArray1, y represent inputArray2, ny represent sizeArray2, and B represent the outputMatrix.
|
||||||||||||||||||
| identityMatrixSize | ssize_t | Number of rows and columns to generate when matrixType is Identity matrix. | ||||||||||||||||||
| inputArray1 | NIComplexNumber [] | Complex vector used to generate a Diagonal matrix, Toeplitz matrix, Vandermonde matrix, or Companion matrix. This matrix must be an array of ComplexNum. The following C typedef statement defines the ComplexNum structure: typedef struct { double real; double imaginary; } ComplexNum; |
||||||||||||||||||
| sizeOfArray1 | ssize_t | Number of elements in vector inputArray1. Because the first vector is used in constructing the Diagonal matrix, Toeplitz matrix, the Vandermonde matrix and the Companion matrix, sizeOfArray1 also determines the size of the generated matrix. | ||||||||||||||||||
| inputArray2 | NIComplexNumber [] | Second vector to use to generate the Toeplitz matrix. This matrix must be an array of ComplexNum. The following C typedef statement defines the ComplexNum structure: typedef struct { double real; double imaginary; } ComplexNum; |
||||||||||||||||||
| sizeOfArray2 | ssize_t | Number of elements in vector inputArray2. | ||||||||||||||||||
| Output | ||||||||||||||||||||
| Name | Type | Description | ||||||||||||||||||
| outputMatrix | void * | Generated matrix as an array of ComplexNum. | ||||||||||||||||||
Return Value
| Name | Type | Description |
| status | AnalysisLibErrType | A value that specifies the type of error that occurred. Refer to analysis.h for definitions of these constants. |
Additional Information
Library: Advanced Analysis Library
Include file: analysis.h
LabWindows/CVI compatibility: LabWindows/CVI 5.0 and later
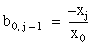 for j = 1, 2, . . ., nx – 1
for j = 1, 2, . . ., nx – 1