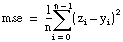GenLSFitCoef
Advanced Analysis Library Only
AnalysisLibErrType GenLSFitCoef (void *hMatrix, ssize_t numberOfRows, ssize_t numberOfColumns, double yArray[], double coefficientArray[], int algorithm);
Purpose
Finds the set of linear fit coefficients, which describe the linear curve that best represents the input data that GenLSFitCoef uses to obtain the least squares solution technique. The general form of the k-dimension linear fit is as follows:
| Let | i = 0, 1, . . ., n be your ith observation |
| xij, ..., xik – 1 be k —1 observed x points | |
| yi be observed y points |
Compose the HMatrix as follows:
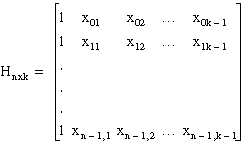
GenLSFitCoef obtains the general LS linear fit coefficient bk by minimizing the quantity:

Parameters
| Input | ||
| Name | Type | Description |
| hMatrix | void * | Input matrix that represents the formula you use to fit the data set (x,y). Hij are the function values of Xi. |
| numberOfRows | ssize_t | Number of rows in HMatrix and the number of elements in YArray. |
| numberOfColumns | ssize_t | Number of columns in HMatrix and the number of elements in coefficientArray. |
| yArray | double [] | Array that contains the y-coordinates of the (x, y) data sets to fit. |
| algorithm | int | Algorithm used to solve the multiple linear regression model. The algorithm has the following possible values.
|
| Output | ||
| Name | Type | Description |
| coefficientArray | double [] | The set of linear coefficients that best fit the multiple linear regression model in a least squares sense. The size of this array must be at least numberOfColumns. |
Return Value
| Name | Type | Description |
| status | AnalysisLibErrType | A value that specifies the type of error that occurred. Refer to analysis.h for definitions of these constants. |
Additional Information
Library: Advanced Analysis Library
Include file: analysis.h
LabWindows/CVI compatibility: LabWindows/CVI 3.1 and later