SpecialMatrix
Advanced Analysis Library Only
AnalysisLibErrType SpecialMatrix (int matrixType, ssize_t identityMatrixSize, double inputArray1[], ssize_t sizeOfArray1, double inputArray2[], ssize_t sizeOfArray2, void *outputMatrix);
Purpose
Generates a special type of real matrix depending on the value of matrixType. There are five possible matrix types: Identity, Diagonal, Toeplitz, Vandermonde, and Companion.
Parameters
| Input | ||||||||||||||||||||
| Name | Type | Description | ||||||||||||||||||
| matrixType | int | The type of matrix to generate. The following table shows each matrix type and its behavior. Let n represent matrixSize, x represent inputArray1, nx represent sizeArray1, y represent inputArray2, ny represent sizeArray2, and B represent the outputMatrix.
|
||||||||||||||||||
| identityMatrixSize | ssize_t | Number of rows and columns to generate when matrixType is an Identity matrix. | ||||||||||||||||||
| inputArray1 | double [] | Complex vector used to generate a Diagonal matrix, Toeplitz matrix, Vandermonde matrix, or Companion matrix. | ||||||||||||||||||
| sizeOfArray1 | ssize_t | Number of elements in vector inputArray1. | ||||||||||||||||||
| inputArray2 | double [] | Second vector to use to generate the Toeplitz matrix. | ||||||||||||||||||
| sizeOfArray2 | ssize_t | Number of elements in vector inputArray2. | ||||||||||||||||||
| Output | ||||||||||||||||||||
| Name | Type | Description | ||||||||||||||||||
| outputMatrix | void * | The generated matrix. | ||||||||||||||||||
Return Value
| Name | Type | Description |
| status | AnalysisLibErrType | A value that specifies the type of error that occurred. Refer to analysis.h for definitions of these constants. |
Additional Information
Library: Advanced Analysis Library
Include file: analysis.h
LabWindows/CVI compatibility: LabWindows/CVI 5.0 and later
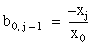 for j = 1, 2, . . ., nx – 1
for j = 1, 2, . . ., nx – 1